Linear regression is a statistical technique to fit a best line through 2D (x,y) data. That is, it finds a line that predicts the y value (dependent variable) using the x value (independent variable). More formally, given data yi, xi, one is trying to find m and c to fit a line of the form y=mx+c. The best values of m and c can be calculated using:
m = σxy / σ2x
c = μy − m μx
where μx and μx are the arithmetic mean of x and y respectively, σ2x is the variance of x, and σxy is the covariance of x and y
Note that the idea of 'best' here means minimising the sum of the squares of the y error, that is minimising:
Σ (yi − mxi+c)2
You get different answer if you swop the variables and look for the regression of x on y.
When there is more than one independent variable, there is an extension, multi-linear regression, which instead fits a hyperplane) to the data.
Used on pages 129, 139, 144, 155, 329
Linear regression for short walks: solid line ignoring the outlier, dotted line including all data.
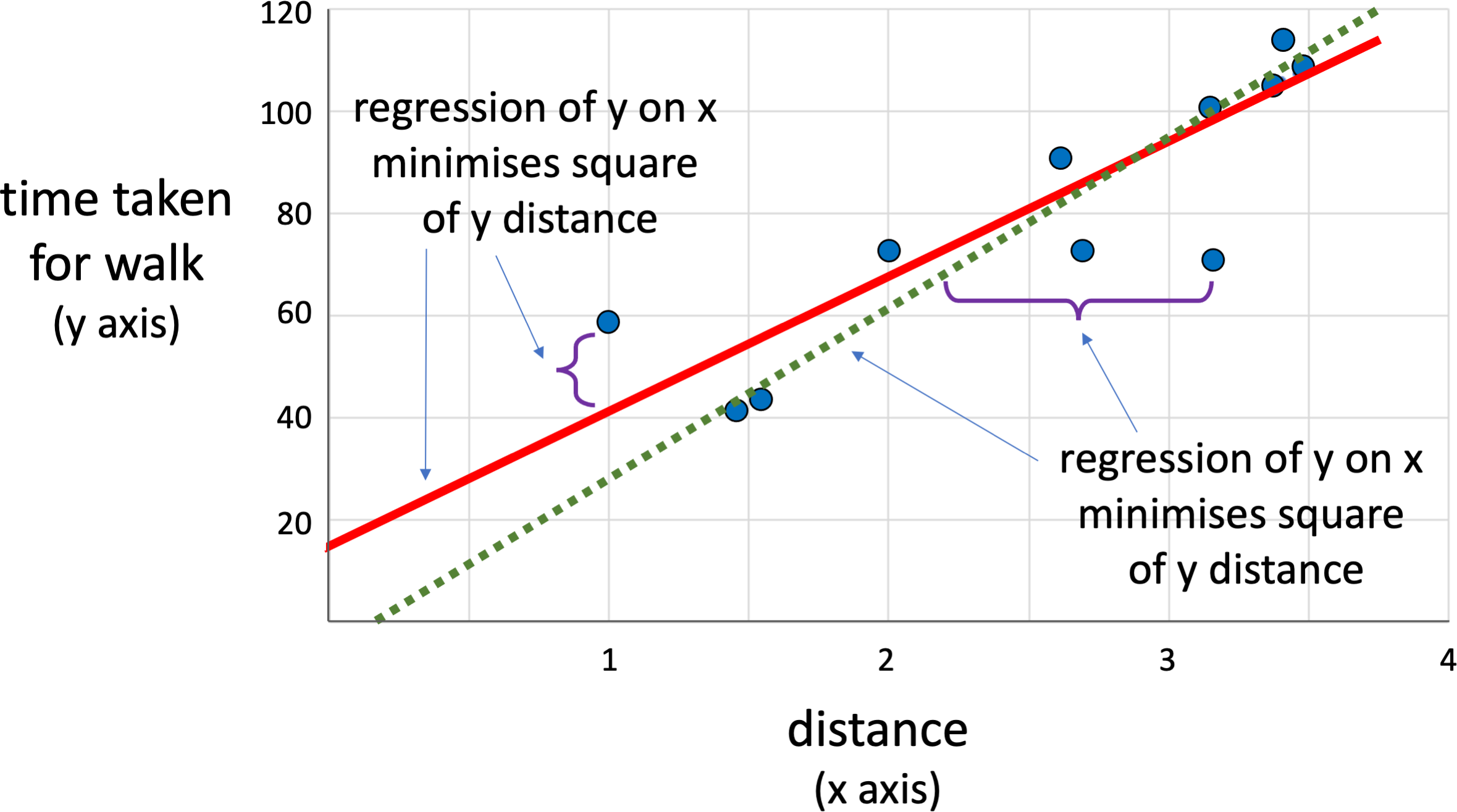
Linear regression as least squares -- different ways to do it